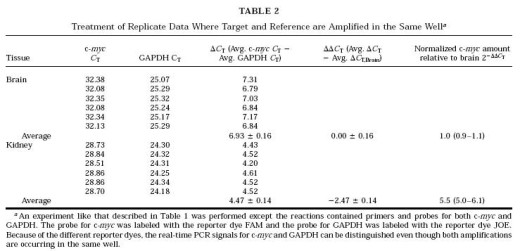
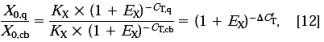在表1 和表2 中,估计误差在从△C
T 到△△C
T 的计算中未见有增加,这是因为我们把参照基因和检测基因的误差都显示出来了。我们把△CT,cb 当作一个人为设定的常数来减去,得到△△CT 。这样得到的结果就与图 2 所显示的在求平均之前对不同重复样本分别通过各自的CT 值求实 所得结果 相当。另一种方法是将参照基因当作没有任何误差的1倍的量,在这种情况下,平均△C
T,cb 的误差值被引入到每一样本的△△C
T中。在表1中,肾脏中△△C
T 变成- 2.50±0.20 而经过校正的c-myc 量是5.6 倍,范围从4.9 到 5.6 。而在大脑中的结果是没有误差的1倍。
2. 2-△Cf方法
2.1. 2-△Cf方法的推导
通过内标RNA 可以对加入 RNA 的量的差异进行校正。2-△△CT方法的数据分析的一个特点就是能够利用实时PCR 实验的一部分数据来完成这种校正。在其它的方法不能定量初始 RNA 量的时候:例如,在能得到的 RNA 量非常有限的时候或者需要处理高通量的样品的时候,这一方法的优势就格外明显。当然我们也可以利用PCR 实验以外的方法来完成这种校正。最常用的一种方法就是用紫外吸收来确定用于cDNA 合成的RNA 量,然後将相同的RNA 反转录产生的cDNA 用于PCR 定量反应。这种外标法校正的一个应用例子就是研究某种实验处理是否影响内标基因的表达。在这里,目标基因和内标合二为一。在这个例子中,公式[2] 不被公式[3] 除,公式[5 ]变成:
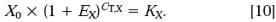
整理得: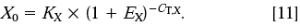 任一样品X0,q 除以参照品X0,cb 得:
任一样品X0,q 除以参照品X0,cb 得: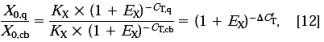
在这里△ C'T=CT,q-CT,cb 。△C’T与前面计算中用的△CT(用目标基因CT值减去参照基因CT值)相互区别。
就象在1.1部分所描述的,如果条件优化较好,效率接近于1,内标相对于参照因子为:

2.2. 2-△Cf方法的应用
2
-△CT'方法的一个应用就是确定实验处理对某一候选内标基因的影响。为了显示这一过程,我们做了
血清饥饿/ 诱导实验(7) 。血清饥饿/ 诱导是研究某些 mRNA 降解的常用方法(8)。然而,血清可能影响一些基因的表达包括标准的看家基因的表达。
在24-h 血清饥饿
培养之後,在NIH 3T3 细胞中加入15% 血清诱导基因表达。从细胞中提取Poly(A)
+ RNA ,并将之反转录成cDNA 。利用SYBR Green 通过实时定量PCR 检测GAPDH ,β 2 -microglobulin cDNA 的量。GAPDH 和β
2 -microglobulin 各自的相对量通过2
-△CT'公式求得。细胞处理对于GAPDH 的基因表达有明显影响,但对β
2 -microglobulin 没有什么影响。因此β
2 -microglobulin 很适合做血清刺激定量实验的内标,而GAPDH并不适合。这一例子向大家展示了在只研究一个基因的时候怎么用2
-△CT'的方法分析基因相对表达数据。
实时PCR 最终分析的是阈值循环或CT。
C
T值通过 PCR 信号的对数值和循环数来确定。因此C
T值是一个指数而非线性概念。因此,在任何统计分析中都不要用原始的C
T值来表示结果。正如我们在前文中所描述的一样,PCR 相对量通常和内标和参照样本一起计算而很少直接用C
T值来表示,除非我们想检验重复样本之间的差别。为了向大家显示这一点,我们用SYBR Green 通过real-time PCR 来检测相同c
DNA 的96 个重复反应。所有反应组分在同一管中混好後分装到 96 个管中,做实时 PCR 分析,得到了每一个样本的 C T 值。为了比较样品间变化,计算了96 个样本的平均±SD,如果通过原始C
T值计算,平均 ±SD 是20.00±0.193,CV 为0.971% 。但是如果把原始C
T 值用2 -CT
转化成线性形式,平均±SD是9.08 × 10
-7 ±1.33 × 10
-7,CV 为13.5 %。从这个简单的例子我们可以看出,通过原始C
T值来反映变化是错误的,应该避免。用2
-CT 将单个数据转化成线性形式来说明重复样本之间的变化和差异更准确可靠。
4. 结论
实时定量PCR 实验设计和数据分析可以采用相对定量和绝对定量两种方法,研究人员在设计实时定量PCR 实验分析
基因表达的时候首先要问的一个问题就是:数据最後会以一个什么样的形式得到。如果需要知道绝对的拷贝数,就必须用绝对定量的方法,否则只需要给出基因表达相对量就足够了。相对定量可能比绝对定量要更容易一些,因为它不需要作标准曲线。
本文所给出的公式对于每个用相对定量的方法分析基因表达差异的研究人员都足够了。下面,我们总结一下实验设计和评估中的一些重要步骤:
选择一个内标基因。
确定内标的有效性,确保它不会受到实验处理的影响。
通过PCR 扩增目标基因和内标基因RNA 或
cDNA 的一系列梯度稀释模板确保它们的扩增效率相同。
最後通过2-△CT 计算将统计数据转化成线性形式而不是原始CT值。
参考文献
1. Murphy, L. D., Herzog, C. E., Rudick, J. B., Fojo, A. T., and Bates, S. E. (1990) Biochemistry 29, 10351–10356.
2. Noonan, K. E., Beck, C., Holzmayer, T. A., Chin, J. E., Wunder,J. S., Andrulis, I. L., Gazdar, A. F., Willman, C. L., Griffith, B.,Von-Hoff, D. D., and Robinson, I. B. (1990) Proc. Natl. Acad. Sci. to a linear form using 2 2 C T more accurately depicts the USA 87, 7160–7164.
3. Horikoshi, T., et al. (1992) Cancer Res. 52, 108–116.
4. Heid, C. A., Stevens, J., Livak, K. J., and Williams, P. M. (1996) Genome Res. 6, 986–994.
5. Winer, J., Jung, C. K., Shackel, I., and Williams, P. M. (1999) Anal. Biochem. 270, 41–9.
6. Schmittgen, T. D., Zakrajsek, B. A., Mills, A. G., Gorn, V., Singer, M. J., and Reed, M. W. (2000) Anal. Biochem. 285, 194–204.
7. Schmittgen, T. D., and Zakrajsek, B. A. (2000) J. Biochem. Biophys.Methods 46, 69–81.
8. Chen, C. Y., and Shyu, A. B. (1994) Mol. Cell. Biol. 14, 8471–8482.
9. Iyer, V. R., et al. (1999) Science 283, 83–87.
10. Giulietti, A., Overbergh, L., Valckx, D., Decallone, B., Bouillon, R., and Mathieu, C. (2001) Methods 25, 386–401.
11. Niesters, H. G. M. (2001) Methods 25, 419–429.
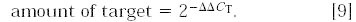

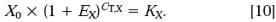
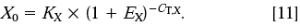 任一样品X0,q 除以参照品X0,cb 得:
任一样品X0,q 除以参照品X0,cb 得: